Linearization of Nonlinear Depth Values in Screen Space
介绍在透视视图时，片段的屏幕空间内非线性化深度值如何进行线性化
Perspective projection Matrix
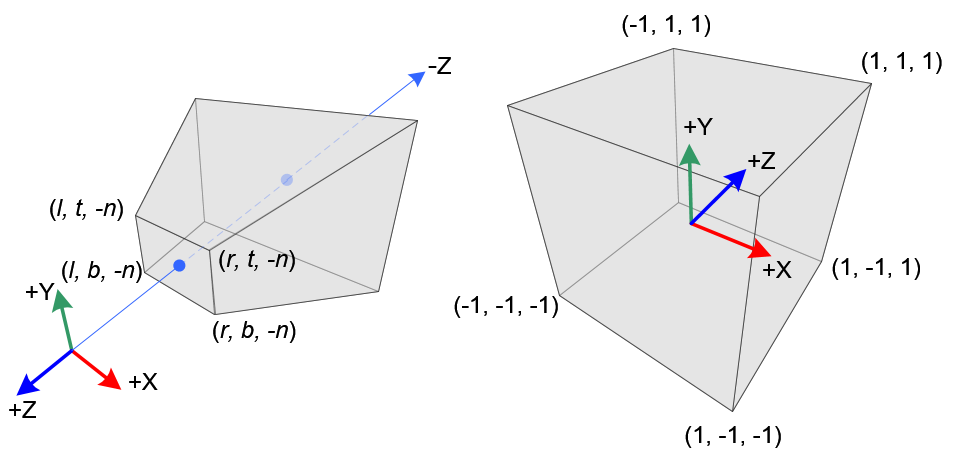Perspective Frustum and Normalized Device Coordinates (NDC)
Note that the eye coordinates are defined in the right-handed coordinate system, but NDC uses the left-handed coordinate system. That is, the camera at the origin is looking along -Z axis in eye space, but it is looking along +Z axis in NDC.
The complete projection matrix $\mathbf{M_{\mathit{projection}}}$ is;
\[\begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ \\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\ \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}\]Depth Linearization
当调试场景的深度时，通常需要将深度值直观地可视化显示出来。而片段着色器中提供的屏幕空间深度值是非线性化的，即它在z值很小的时候有很高的精度，而 z 值很大的时候有较低的精度。片段的深度值会随着距离迅速增加，所以几乎所有的顶点的深度值都是接近于 1.0 的。将深度值显示在屏幕上时，你可能会注意到所有东西都是白色的，看起来就像我们所有的深度值都是最大的 1.0。这非常不利于观察，需要我们将其线性化。一种可行的方式是求出摄像机空间内片段的 z 值，然后将其可视化出来。
局部空间、世界空间和摄像机空间中顶点坐标的 $w$ 分量不会被变换矩阵修改，总是为 1.0。只有在经历透视投影变换后顶点坐标的 $w$ 分量才会被修改，也就是在裁剪空间中顶点坐标的 $w$ 分量才可能是 1.0 以外的值。假设当 $w_{view}=1.0$ 时顶点在摄像机空间的坐标为 $\mathbf{V_{\mathit{view}}}=(x_{view}, \ y_{view}, \ z_{view}, \ w_{view})=(x_{view}, \ y_{view}, \ z_{view}, \ 1.0)$，对应的在裁剪空间和 NDC 中的坐标分别为 $\mathbf{V_{\mathit{clip}}}=(x_{clip}, \ y_{clip}, \ z_{clip}, \ w_{clip})$ 和 $\mathbf{V_{\mathit{ndc}}}=(x_{ndc}, \ y_{ndc}, \ z_{ndc}, \ w_{ndc})$。摄像机空间坐标按如下方式转换到裁剪空间坐标：
\[\underbrace{ \begin{pmatrix} x_{clip} \\ \\ y_{clip} \\ \\ z_{clip} \\ \\ w_{clip} \end{pmatrix} }_{\mathbf{V}_{clip}} = \underbrace{ \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ \\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\ \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} }_{\mathbf{M}_{projection}} \ \underbrace{ \begin{pmatrix} x_{view} \\ \\ y_{view} \\ \\ z_{view} \\ \\ 1.0 \end{pmatrix} }_{\mathbf{V}_{view}} \tag{1}\]令 $\mathbf{M_{\mathit{projection}}}$ 中 $ \frac{-(f+n)}{f-n} = A $，$\frac{-2fn}{f-n} = B$，$f$ 和 $n$ 为摄像机空间内视锥体远近平面的 $z$ 值。则有：
\[z_{clip} = Az_{view}+B \tag{2}\]那么：
\[z_{view} = \frac{z_{clip} - B}{A} \tag{3}\]因 $z_{clip}$ 未知，下面求取 $z_{clip}$。由透视除法可知：
\[z_{ndc} = \frac{z_{clip}}{w_{clip}} \tag{4}\]可得：
\[z_{clip} = w_{clip}z_{ndc} \tag{5}\]从式 (1) 中还可看出 $w_{clip} = -z_{view}$。则有：
\[z_{clip} = -z_{view}z_{ndc} \tag{6}\]因 $z_{ndc}$ 未知，下面求取 $z_{ndc}$。由视口变换可知：
\[z_{wnd} = \frac{farVal - nearVal}{2}z_{ndc} + \frac{farVal + nearVal}{2} \tag{7}\]当 glDepthRange 函数指定 farVal = 1.0，nearVal = 0.0 时（默认值，这指定的是屏幕空间深度值范围，与摄像机空间的 $f$ 和 $n$ 不同）：
\[z_{wnd} = \frac{z_{ndc} + 1}{2} \tag{8}\]那么：
\[z_{ndc} = 2z_{wnd} - 1 \tag{9}\]将式 (9) 代入式 (6)，可求得：
\[z_{clip} = -z_{view} \times (2z_{wnd} - 1) \tag{10}\]将式 (10) 代入式 (3) 最终可求得：
\[\begin{aligned} z_{view} &= \frac{-B}{(2z_{wnd}-1) + A} \\ &= \frac{-\frac{-2fn}{f-n}}{(2z_{wnd}-1) + \frac{-(f+n)}{f-n}} \\ &= \frac{\frac{2fn}{f-n}}{(2z_{wnd}-1) - \frac{(f+n)}{f-n}} \\ &= \frac{2fn}{(2z_{wnd}-1)(f-n)-(f+n)} \\ &= \frac{-2fn}{(f+n)-(2z_{wnd}-1)(f-n)} \end{aligned} \tag{11}\]因为 NDC 使用左手坐标系，摄像机空间坐标使用右手坐标系，涉及到左右手坐标系的变化，所以实际的摄像机空间坐标值分量 $z_{view}$ 是上面结果的负值：
\[\begin{aligned} z_{view} &= -1 \times \frac{-2fn}{(f+n)-(2z_{wnd}-1)(f-n)} \\ &= \frac{2fn}{(f+n)-(2z_{wnd}-1)(f-n)} \end{aligned} \tag{12}\]最后，由于片段在摄像机空间坐标值分量 $z_{view}$ 的取值范围在 [$n$, $f$] 之间，要将其作为片段的颜色输出到屏幕上，需要对其归一化：
\[\frac{z_{view} - n}{f - n} \tag{13}\]当 $n$ 非常小或 $n$ 与 $f$ 之间相差特别大时，上式可简化为：
\[\frac{z_{view}}{f} \tag{14}\]